Grigori Perelman proposed a solution to the Poincaré conjecture (2003)
the AKS primality test (2002)
the Millennium Prize Problems (May 24, 2000)

the Mandelbrot set (1982)
the butterfly effect (1963)
R.A. Fisher's Statistical Methods for Research Workers (1925)
the Kakeya needle problem (1917)
Minkowski space (1908)

the Archimedes Palimpsest (1906)
the Koch snowflake (1904)
Ergodic theory (early 1900s) was the forerunner of Chaos theory
Hadamard's billiards (1898)
Cayley tables (1889)
Vector analysis (1880)
Georg Cantor established principles of mathematical set theory (1874)
Betti numbers (1871)
the Möbius strip (1858)
Riemannian geometry (1854)
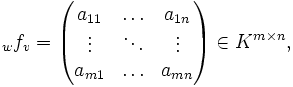
the term "matrix" was coined (1848) by J. J. Sylvester
the existence of transcendental numbers was first proved (1844) by Joseph Liouville
Group theory (1832)
non-Euclidean geometry (1826) was developed by Nikolai Ivanovich Lobachevsky
the Abel–Ruffini theorem (1824)
Bessel functions (1817)
the metric system (1791)
Joseph Louis Lagrange's Mécanique Analytique (1788)
the imaginary number i (1777) was introduced by Leonhard Euler
![]()
Euler's identity (1748)
the f(x) function symbol (1734) was introduced by Leonhard Euler
Leonhard Euler started to use the letter e (1727) for the base of the natural logarithm
Abraham de Moivre's Doctrine of Chances (1718)
Jakob Bernoulli's Ars Conjectandi (1713)

the Newton vs. Leibniz calculus controversy (1709-1716)
Newton's Tractatus de Quadratura Curvarum (1693) was published in 1704 as an appendix to his Optiks
Gottfried Leibniz' Nova methodus pro maximis et minimis (1684)
Gottfried Leibniz invented calculus (November 11, 1675)
the fundamental theorem of calculus (1670)
Athanasius Kircher's Organum mathematicum (1668)
Newton discovered the generalised binomial theorem (1665)
Projective geometry (1639) was founded by Gérard Desargues
the Folium of Descartes (1638)
Fermat's Last Theorem (1637)
the coordinate system (1637)
Henry Briggs' Arithmetica Logarithmica (1624)
John Napier's logarithms (1614)
Bartholomaeus Pitiscus is credited with inventing the decimal point in his trigonometrical tables (1612)
it was subsequently accepted by John Napier in his logarithmic papers
François Viète started the use of letters to represent variables (1591)
![]()
Simon Stevin's La Theinde (1585)
François Viète's Canon mathematicus seu ad triangula (1579)
Francesco Maurolico's Arithmeticorum libri duo (1575) includes one of the first known proof by mathematical induction

Rafael Bombelli published L'Algebra parte maggiore dell'aritmetica (1572) the first systematic
examination of imaginary numbers (numbers that are multiples of i, where i is the square root of -1)
the = sign was introduced (1557) by Robert Record
Adam Riese's Rechnung nach der lenge auff der Linihen und Feder (1550)
Albrecht Dürer's Underweysung der Messung (1525)

Gregor Reisch's Margarita Philosophica (1503)

Luca Pacioli's Summa de arithmetica, geometrica, proportioni et proportionalita (1494)

the arithmetic symbols for addition and subtraction (1489) were invented by Johannes Widmann
Nicholas of Cusa's coincidence of opposites (1430)
Richard of Wallingford's Quadripartitum de sinibus demonstratis (14th century) was the first original Latin treatise on trigonometry
Gersonides' Book of Numbers (1321)

Fibonacci's Liber Abaci (1202)
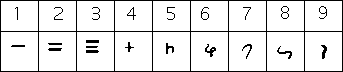
the Latin translation of al-Khwarizmi's book On the Calculation with Hindu Numerals (twelveth century)
introduced the use of the positional number system and the number zero to Europe
Bhaskara (1150) developed differential calculus
a special case of the mean value theorem (12th century) was first elucidated by Indian astronomer Bhaskara
Omar Khayyám's writings (1100) on Algebraic geometry
Al-Jayyani, an Arabic scholar in Moorish Spain (1060) wrote the first treatise on spherical trigonometry
Gerbert d'Aurillac's Mathematical writings (end of the 10th century)
al-Ma'mun's House of Wisdom (825)
x² + 10x = 39
x² + 21 = 10x
3x + 4 = x²
Algebra (820) is derived from operations described in the treatise written by the Persian mathematician Al-Khwarizmi
![]()
0
the earliest known text to treat zero as a number in its own right (628) was Brahmagupta's
Brahma Sphuta Siddhanta (The Opening of the Universe), a work on astronomy and mathematics,
which gives methods to solve quadratic equations, sum series, and compute square roots
the mathematician-astronomer Aryabhata first used infinitesimals (499) and
expressed an astronomical problem in the form of a basic differential equation
Theon of Alexandria's translation of Euclid's Elements (364)
Pappus of Alexandria wrote Synagoge (Collections) (340) a guide to Greek geometry
Liu Hui calculated the value of pi as 3.14159 (263) which is correct, to five decimal places in his book with solutions to
mathematical problems presented in the famous Chinese book of mathematics the Nine Chapters on the Mathematical Art
Diophantus' Arithmetica (250)
Nicomachus' Introduction to Arithmetic (100)
the Nine Chapters on the Mathematical Art (1st century)
Hipparchus (150 bc) was the first to compile a trigonometric table, which allowed him to solve any triangle
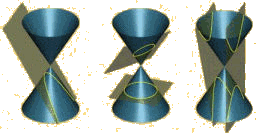
Apollonius of Perga (230 bc) gave the ellipse, the parabola, and the hyperbola the names by which we know them.
22⁄7 (240 bc)
Hindus in India develop the Arabic system of number notation (260 bc)
perfect numbers (3rd century bc)

Euclid's Elements (early 3rd century bc)
Menaechmus (4th century bc) discovered conic sections
Archytas founded the study of mathematical mechanics (4th century bc)
Theaetetus' work in mathematics (390 bc)
Hippocrates' squaring of Lunes (450 bc)
Antiphon's method of exhaustion (450 bc)



Theano's most important work (520 bc) is said to have been a treatise on the principle of the golden mean
the Rhind papyrus (1800 bc)
25⁄8 (19th century bc)

writing on tablets, Babylonian mathematicians (2000 bc) solve quadratic equations
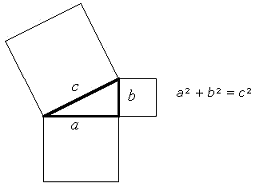
and demonstrate their discovery of what is now called the Pythagorean theorem
the Moscow Mathematical Papyrus (2000 bc)
magic squares (2800 bc)
a sexagesimal (base-sixty) numeral system (3000 bc) was used by the ancient Sumerians